摘要:
碳纤维复合材料具有密度小、弹性高和韧性好等特点,被广泛应用于航空航天和汽车工业等领域。由于碳纤维复合材料制作工艺的复杂性和不稳定性以及服役期间易受环境的影响,易产生分层、孔隙、纤维褶皱等各种类型的损伤。介绍了基于体波或导波的C扫描、相控阵、空气耦合、激光超声、光纤超声检测技术的原理、特点以及用于碳纤维复合材料损伤检测的研究现状。综述了最具有代表性的损伤诊断成像算法,包括全聚焦成像、三维可视化成像、层析成像、逆时偏移成像和概率成像方法,这些成像方法能够有效地实现碳纤维复合材料各种类型的损伤形貌图像。从建立复杂构件的碳纤维复合材料层合板的阵列声场模型、优化损伤成像算法、构建智能/高效/实时化的结构健康监测成像系统、建立损伤定量评估标准、结合机器学习和数字孪生技术实施损伤诊断评估和寿命预测等方面进行了展望。碳纤维复合材料具有高强度,高模量,良好的抗疲劳性能和抗腐蚀性能等,被广泛应用于航空、航天、汽车工业等领域。在航空领域,碳纤维复合材料有利于飞机结构的轻质化性能的提高,是民用飞机的主要组成材料之一。在航天领域,碳纤维复合材料的隔热、耐高温等特殊功能在飞行器、卫星、宇航器、固体火箭发动机和导弹壳体结构中,发挥着重要的作用。在汽车工业领域,随着低成本的制作工艺的发展,使得具有减震效果和大规模整体成型等优点的先进碳纤维复合材料,在汽车工业领域呈现出蓬勃发展的势头。1 碳纤维复合材料的声学模型
碳纤维复合材料层合板是由多个具有不同纤维取向的碳纤维层按照一定顺序堆叠固化形成的。根据碳纤维复合材料结构的特性,目前的研究工作将超声在其中的传播模型分为两种,分别为基于体波在厚度方向或导波在面内方向检测的声学模型。在工业检测领域,通常将碳纤维复合材料在厚度方向上简化为各向同性介质,如图3所示的xz平面,采用单探头以垂直入射的方式测量的声速为碳纤维复合材料的恒定声速。
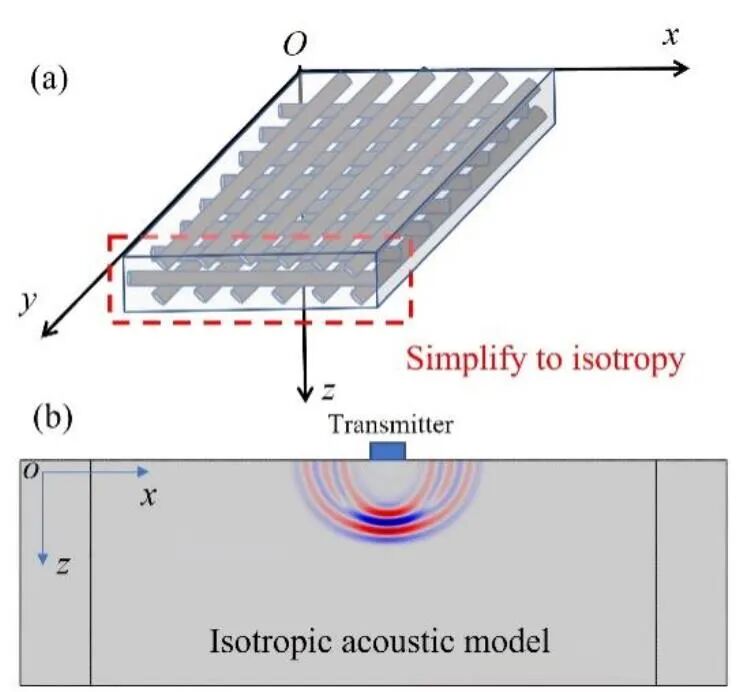
Fig. 3 Isotropic acoustic model for carbon fiber composites based on body wave detection然而,若采用超声阵列检测技术,对于不同铺层方向堆叠的多向碳纤维复合材料层合板的检测,不可避免地出现斜入射的声传播路径。若基于各向同性声学模型进行检测,易造成损伤的误检和漏检。在常用的超声波频率(1~10 MHz)下的波长(0.3~3 mm)大于碳纤维复合材料的每层厚度(0.125~0.25 mm)。因此,如图4(a)所示,可通过合成射线追踪模型推导出的等效慢度面来获得等效刚度常数,建立均质化声学模型。通过底面反射法和穿透法,可获取此模型在厚度方向上的速度分布曲线如图4(b)所示。

图4 均质化声学模型示意图(a)[6]和速度分布曲线(b)Fig. 4 Schematic diagram of the homogenization acoustic model (a)[6] and velocity distribution curve (b)虽然基于射线理论的均质化声学模型将碳纤维复合材料多向板所包含的整体均质化,从而简化了计算过程。然而,该模型忽略了声波在碳纤维复合材料多层结构中的反射和折射现象,从而降低了识别和定位损伤的精度。在考虑碳纤维复合材料的各向异性和多层结构的影响下,建立非均质化的各向异性声学模型。对于单向铺层的碳纤维复合材料,超声波在其中的传播符合各向异性弹性波的传播规律。可根据弹性波动方程推导出Christoffel方程,Christoffel方程用于表征相速度和群速度的分布。该方程表明了声速空间分布与材料弹性刚度系数矩阵直接相关,Christoffel方程[8]如下:

其中,ρ是介质密度,c是相速度,δijδij是Kronecker delta符号,Γij=CijlmninjΓij=Cijlmninj是Christoffel矩阵,uiui是质点位移,CijlmCijlm是4阶弹性刚度张量(i, j, l, m=1,2,3),n1,n2和n3n1,n2和n3是声传播单位矢量的分量。通过求解Christoffel方程,可以得到关于相速度的三个解,分别对应准纵波(qP波),准垂直剪切波(qSV波)以及准水平剪切波(qSH波)三种波型。与各向同性介质不同的是,各向异性介质中的相速度与群速度在传播方向和大小均不相同。图5(a)为碳纤维铺层角度分别为0°、±45°、90°方向的准纵波(qP波)群速度空间分布。

Fig. 5 Anisotropic acoustic model for carbon fiber composites based on body wave图5(b)为基于各向异性声学模型的声传播示意图。从图中可以明显看出,由于准纵波在不同方向铺层中传播时,垂直传播的声速相一致。因此,在垂直传播的方向没有层间反射和折射,反之,在偏离垂直方向的波产生了多次反射和折射的结构噪声。超声导波是由超声波在边界区域发生多次反射、折射并相互叠加而形成的。超声导波不仅与材料参数相关,还与边界条件有关,这导致超声导波比传统超声体波更加复杂,具有多模态和频散特性,例如板中传播的Lamb波。Lamb波有对称模态和反对称模态。理论上,因复合材料层合板的各向异性,Lamb波在复合材料中的传播特性与方向有关。然而,如果选用足够多的不同碳纤维方向的铺层获得的层合板可以被视为准各向同性模型。例如,碳纤维复合材料的叠层顺序为[0/90/-45/45]2可视为准各向同性复合材料板。考虑碳纤维复合材料的各向异性,波在碳纤维复合材料层合板中的传播出现了复杂的现象,如相速度和群速度方向不一致。在N层复合材料层合板中,各层内的波满足Navier位移方程:
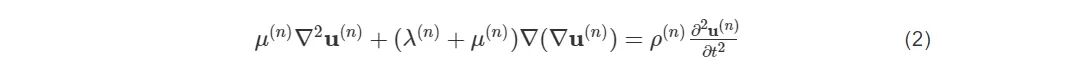
式中n=1,2,3...,N,ρn,λn和μnn=1,2,3...,N,ρn,λn和μn是第n层的密度和拉梅常数。如图6所示,碳纤维复合材料的上下边界为自由边界条件,各层为刚性连接,可获得频散方程为:
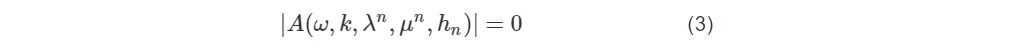

图6 基于导波的碳纤维复合材料各向异性声学模型
Fig. 6 Anisotropic acoustic model for carbon fiber composites based on guided wave
通常采用有限元法、半解析有限元法、传递矩阵法 、全局矩阵法和谱元法等求解复合材料中导波传播特性。虽然有限元方法易于实现,且能够适用于多个铺层方向的碳纤维复合材料层合板,但是其计算时间太长。目前常采用传递矩阵法和全局矩阵法,传递矩阵法使用起来较为方便,但是在大频厚积易于出现数值不稳定现象,可采用全局矩阵法以消除不稳定的现象,张海燕等将全局矩阵法应用于碳纤维复合材料层合板中的超声导波的传播特性的分析中。此外,Li等采用谱元法研究了三种不同铺层形式的碳纤维复合材料层合板的导波传播问题,研究结果表明反对称模态更适合用于识别碳纤维复合材料结构中的分层损伤。除此之外,He等采用数学近似的Legendre正交多项式方法推导和求解了各向异性复合材料层合板的导波方程。
研究人员针对复合材料中的导波衰减问题开展了一系列研究,包括衰减模型研究和导波衰减问题研究等。衰减模型有Hyteretic模型、Rayleigh模型和Kelvin-Voigt模型。Gresil等采用Rayleigh衰减模型探究了碳纤维复合材料层合板中的导波衰减问题。对于Kelvin-Voigt衰减模型,Shen等和Mei等开展了复合材料板中理论和实验研究,实验验证了该衰减模型的准确性。










